Core User Guide: Traverse Your Graph

Graph traversals are invoked by means of a Traverser that extends scala.collection.Traversable in turn. This may happen

directly to allow fine-grained control or
under the hood whenever you call a "high level" method like findCycle.

Needless to say, all methods relying on recursion are tail recursive.

The examples below make use of

import scalax.collection.edges._
import scalax.collection.edges.labeled._
import scalax.collection.generic.AnyEdge
import scalax.collection.OuterImplicits._
import scalax.collection.immutable.Graph // or mutable

Traverse for a specific node, a path or a cycle

Mostly you are solely interested in the result of a graph traversal such as a specific node, a path or cycle rather than in tracking visited elements. Chances are good that you will find a method that meets your requirement out of the box.

Playing around with the weighted mixed graph along with a lookup function

val g = Graph[Int, AnyEdge](
  1 ~ 2 % 4,
  2 ~ 3 % 2,
  1 ~> 3 % 5,
  1 ~ 5 % 3,
  3 ~ 5 % 2,
  3 ~ 4 % 1,
  4 ~> 4 % 1,
  4 ~> 5 % 0)
def n(outer: Int): g.NodeT = g get outer

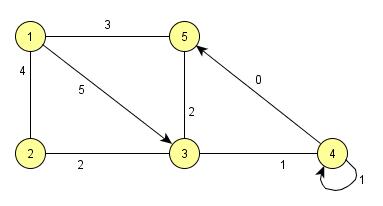
you can do

n(1) findSuccessor (_.outDegree >  3) // Option[g.NodeT] = None
n(1) findSuccessor (_.outDegree >= 3) // Option[g.NodeT] = Some(3)
n(4) findSuccessor (_.edges forall (_.undirected)) // Some(2)
n(4) isPredecessorOf n(1)             // true 
n(1) pathTo n(4)                      // Some(Path(1, 1 ~> 3 % 5, 3, 3 ~ 4 % 1, 4))
n(1) pathUntil (_.outDegree >= 3)     // Some(Path(1, 1 ~> 3 % 5, 3))

val maybeP = n(3) shortestPathTo n(1) // Some(Path(3, 3 ~ 4 % 1, 4, 4 ~> 5 % 0, 5, 1 ~ 5 % 3, 1))
val p = maybeSp.get                   // here we know that maybeP is defined
p.nodes                               // List[g.NodeT] = Nodes(3, 4, 5, 1)
p.weight                              // Double = 4.0

def negWeight(e: g.EdgeT): Float = 5.5f - e.weight
val maybeNegP =
    n(3) shortestPathTo (n(1), negWeight) // Some(Path(3, 2 ~ 3 % 2, 2, 1 ~ 2 % 4, 1))
maybeNegP.map(_.nodes.toList)             // Option[List[g.NodeT]] = Some(List(3, 2, 1))
maybeNegP.map(_.weight)                   // Option[Double] = Some(6.0)

val maybeSubgraphP1 = n(4).withSubgraph(nodes = _ < 4) pathTo n(2)
	                                        // Some(Path(4, 3 ~ 4 % 1, 3, 2 ~ 3 % 2, 2))
maybeSubgraphP1.map(_.nodes.toList)       // Option[List[g.NodeT]] = Some(List(4, 3, 2))

val maybeSubgraphP2 = n(4).withSubgraph(edges = _.weight != 2) pathTo n(2)
                                          // Some(Path(4, 4 ~> 5 % 0, 5, 1 ~ 5 % 3, 1, 1 ~ 2 % 4, 2))
maybeSubgraphP2.map(_.nodes.toList)       // Some(Nodes(4, 5, 1, 2))

As to

Searches for any (direct or indirect) successor of node 1 having outDegree > 3 and finds None.
Searches for any successor of node 1 having outDegree >= 3 and finds node 3.
Searches for any successor of node 4 having only undirected edges and finds node 2.
Successfully tests for node 4 being a predecessor of node 1.
Finds an arbitrary path from node 1 to node 4.
Finds a path from node 1 to an arbitrary node having outDegree >= 3.
Determines the shortest path from node 3 to node 1.
Gets the path of type g.Path.
Reduces path p to the nodes on the path.
Among others, g.Path supports weight to calculate the total of the edge weights on the path.
Defines a custom weight function to override static edge weights. Using float demonstrates that the weight method may return any numeric type.
Calls shortestPathTo with the above custom weight function negWeight. The returned path is the longest one in terms of static edge weights as 5.5f exceeds the maximum static weight.
Note that the weight of the returned path does not reflect the custom weights used to calculate the shortest path but just the static weights of the edges on the path.
Finds a path from node 4 to node 2 by restricting the traversal to a subgraph containing only nodes with value less than 4.
Finds a path from node 4 to node 2 by restricting the traversal to a subgraph containing only edges with weight of 2.

val g = Graph(1 ~> 2, 1 ~> 3, 2 ~> 3, 3 ~> 4, 4 ~> 2)
val fc1 = g.findCycle         // Some(Cycle(3, 3 ~> 4, 4, 4 ~> 2, 2, 2 ~> 3, 3))
val fc2 = (g get 4).findCycle // Some(Cycle(4, 4 ~> 2, 2, 2 ~> 3, 3, 3 ~> 4, 4))

for (c1 <- fc1; c2 <- fc2) yield c1 == c2     // false
for (c1 <- fc1; c2 <- fc2) yield c1 sameAs c2 // true

g.findCycleContaining(g get 1)                // None

As to

Finds an arbitrary cycle in g, if any.
Finds an arbitrary cycle reachable from node 4, if any. Node 4 does not necessarily lies on the path.
c1 and c2 are not equal because they start at different nodes.
Even so, c1 and c2 depict the same cycle in a semantic sense.
There exists no cycle containing node 1.

Cycle detecting works for directed, undirected and mixed graphs, alike.

Refine traversers by properties

You may have noticed a call of withSubgraph above. We also refer to such methods, all prefixed by with, as fluent traverser properties since they encourage a fluent way of method calls. You can refine any Traverser by means of the following properties:

Table: Traversal properties.
Property	Factory method	Sample Value	See
`kind: Kind`	`withKind`	`DepthFirst`	members of `Parameters`
`direction: Direction`	`withDirection`	`Successors`	members of `Parameters`
`maxDepth: Int`	`withMaxDepth`	`30`	members of `Parameters`
`maxWeight: MaxWeight`	`withMaxWeight`	`125.3`	members of `FluentProperties` and subclasses of `Properties`
`nodes: (NodeT) => Boolean, edges: (EdgeT) => Boolean`	`withSubgraph`	`_.inDegree < 10`	members of `FluentProperties` and subclasses of `Properties`
`ordering: GraphTraversal.ElemOrdering`	`withOrdering`	`myOrdering`	members of `FluentProperties` and subclasses of `ElemOrdering`

For instance, to exclude a specific node from the traversal in a lazy manner you'd call withSubgraph like

(g get 1).withSubgraph(nodes = _ != 2) pathTo (g get 4)

For more examples on how to make use of properties, check out TraversalSpec.scala

Ordering

As a special case, assume you want to control the order of edges during traversal. You can do so by setting the ordering property. Let's look at an example where we ensure that edges are traversed in reverse order of their weights:

val root = 1
val g = Graph(
	root ~> 4 % 2,
	root ~> 2 % 5,
	root ~> 3 % 4,
  3 ~> 6 % 4,
	3 ~> 5 % 5,
	3 ~> 7 % 2)

def edgeOrdering = g.EdgeOrdering(g.BaseInnerEdge.WeightOrdering.reverse.compare _)
val traverser    = (g get root).outerNodeTraverser.withOrdering(edgeOrdering)
 
traverser.toList  // List(1 to 7: _*)

Traverse for elements

Traversers also enable to inspect graph elements (nodes and/or edges) during the traversal. By doing so they ensure that the passed visitor method is called once and only once for each visited element. As a side note, DownUpTraversers are different in that they call the visitor twice.

Depending on what graph elements you're interested in, select one of the following Traverser factory methods:

Table: Traverser factory methods.
Factory Method	Type of Visitor
`innerNodeTraverser`	path dependent `NodeT`
`outerNodeTraverser`	`N` type parameter of the graph
`innerEdgeTraverser`	path dependent `EdgeT`
`outerEdgeTraverser`	`E[N]` based on the type parameters of the graph
`innerElemTraverser`	`InnerElem`, the common base of `NodeT` and `EdgeT`
`outerElemTraverser`	`OuterElem[N,E]`, the common base of `N` and `E[N]`
`innerNodeDownUpTraverser`	`(Boolean, NodeT)`
`outerNodeDownUpTraverser`	`(Boolean, N)`

While inner elements provide graph functionality at your fingertips, outer elements feel more natural since they're exactly what you passed to the graph.

The above factory methods are available both at node and graph level. At node level root, the node to start the traversal at, is set to the specific node you are invoking the method on; at graph level root must be passed explicitly. In addition you may pass any traverser property to override the default values:

val g = Graph(1 ~> 2 % 1, 1 ~> 3 % 2, 2 ~> 3 % 3, 3 ~> 4 % 1)
val n1 = g get 1

n1.outerNodeTraverser.sum                 // 10
g.outerNodeTraverser(n1).sum              // 10
n1.outerNodeTraverser.withMaxDepth(1).sum //  6
n1.innerEdgeTraverser.map(_.weight).sum   //  7
n1.innerElemTraverser
  .filter {
    case g.InnerNode(n, _) => n.degree > 1
    case g.InnerEdge(_, e) => e.weight > 1
  }
  .map {
    case g.InnerNode(_, n) => n
    case g.InnerEdge(_, e) => e
  }
  .toSet                                  // Set(1, 2, 3, 1 ~> 3 % 2, 2 ~> 3 % 3)

As to

Starts a traversal by outer nodes at n1 to sum up the node values.
The same traversal as before invoked at graph level.
The same traversal as before but restricted up to a depth of 1.
Calculates the sum of weights over all edges. Here we could employ outerEdgeTraverser as well.
Traverses g for all its elements reachable from n1 to return a set of InnerElems with nodes having a degree greater than 2 and edges having a weight greater than 1.
g.InnerNode respectively g.InnerEdge extract both the inner and the outer element.

Visit elements down and up

Assume you'd like to traverse a graph, especially a tree, in a stack-like manner because you need to carry out one action when touching a node the first time and another action when touching the same node the second time in course of traversing up in an imaginary tree. For this purpose you may utilize innerNodeDownUpTraverser:

import scala.collection.mutable.ArrayBuffer

val root = "A"
val g = Graph(root ~> "B1", root ~> "B2")
val innerRoot = g get root
val result = innerRoot.innerNodeDownUpTraverser.foldLeft(ArrayBuffer.empty[String]) { (buf, param) =>
  param match {
    case (down, node) =>
      if (down) buf += (if (node eq innerRoot) "(" else "[") += node.toString
      else buf += (if (node eq innerRoot) ")" else "]")
  }
}
result.fold("")(_ + _) // "(A[B1][B2])" or "(A[B2][B1])"

Extend visitors

In case you need to process the internal state of a traversal including the count of visited nodes, the current search depth, the internal stack etc. extended visitors come in handy. Beware that these are implementation specific:

val g = Graph(1 ~> 2, 1 ~> 3, 2 ~> 3, 3 ~> 4, 4 ~> 2)

import g.ExtendedNodeVisitor
type ValDepth = (Int, Int)
var info = List.empty[ValDepth]

(g get 1).innerNodeTraverser.foreach {
  ExtendedNodeVisitor((node, _, depth, _) => info :+= (node.outer, depth))
}
info.sortWith((a: ValDepth, b: ValDepth) =>
  a._1 < b._1 ||
    a._1 == b._1 && a._2 < b._2
) // List((1, 0), (2, 1), (3, 1), (4, 2)))

Combine queries with visitors

You can also append a visitor to any traversal for a result like a path or cycle like:

val g = Graph(1 ~> 2, 1 ~> 3, 2 ~> 3, 3 ~> 4, 4 ~> 2)
var center: Option[g.NodeT] = None

val maybeCycle = (g get 4).findCycle( n =>
  center = center match {
    case s @ Some(c) => if (n.degree > c.degree) Some(n) else s
    case None        => Some(n)
  }
)
maybeCycle.map(_.sameElements(List(2, 2 ~> 3, 3, 3 ~> 4, 4, 4 ~> 2, 2))) // Some(true)
center                                                                   // Some(2)

The above expression evaluates to an Option[Path]. In course of the traversal the appended visitor also calculates the node with the maximum degree among those visited. The resulting center need not be part of the cycle.

Find components

You can search for weakly or strongly connected components. In both cases you first need to decide on where the search should start:

Starting at graph level ensures that all components of the graph will be returned.
If you start at a specific node you will get all components reachable from that node. This means you will not necessarily get all the components you would get if you started at graph-level.

Find weakly connected components

val componentEdges = {
  def edges(i: Int) = List(i ~> (i + 1), i ~> (i + 2), (i + 1) ~> (i + 2))
  (edges(1), edges(5))
}
val disconnected = Graph.from(edges = componentEdges._1 ++ componentEdges._2)
val sums =
    for (component <- disconnected.componentTraverser())
      yield component.nodes.foldLeft(0)((cum, n) => cum + n.outer) // List(6, 18)

As to

Creates a disconnected graph with two components.
The elements of sums correspond to the sums of the integer node values per component.

Here is how to search for the weak comopnent containing a specific node:

val anyNode = disconnected.nodes.draw(new util.Random)
anyNode.weakComponent.nodes // componentEdges._1.size = 3

Find strongly connected components

Strongly connected components are computed based on a tail-recursive version of Tarjan's algorithm.

Let us refer to the sample graph on Wikipedia:

type G = Graph[Char, DiEdge[Char]]
val sccExpected: (G, G) = (
  Graph('a' ~> 'b', 'b' ~> 'c', 'c' ~> 'd', 'd' ~> 'a', 'd' ~> 'e', 'c' ~> 'e', 'e' ~> 'c'),
  Graph('f' ~> 'g', 'g' ~> 'f', 'g' ~> 'h', 'h' ~> 'j', 'j' ~> 'i', 'i' ~> 'g', 'i' ~> 'f', 'f' ~> 'i')
)
val connected = (sccExpected._1 union sccExpected._2) concat List('e' ~> 'f')
val scc       = connected.strongComponentTraverser().map(_.toGraph)
scc.toSet == Set(sccExpected._1, sccExpected._2) // true

As to

The graph is composed by two strong components connected by a simple directed edge.
The graph-level traverser yields the strong components that we lift to graphs.
Check that the strong components found equal to the expected ones.

To limit the scope of the search to nodes reachable from a give node, start the search at that node like

val startAt = sccExpected._2.nodes.head
startAt.strongComponents.size // 1
startAt.innerNodeTraverser.strongComponents(println)

As to

If we start at a node of the second component, we get just that component.
In case you are interested in the visited elements during the search invoke the search on a traverser.

To the type `Component`

What about the type returned by a component search? Component is a strict set of the nodes and a lazy set of the contained edges. Also, you may invoke toGraph on a component.

Sort topologically

Graph for Scala comes with three flavors of topological sorting along with a remarkably informative result type. For the following examples, assume graph is of type Graph and root is of type graph.NodeT.

Sort on graph level

As a matter of course, you can call topologicalSort directly on your graph instance:

graph.topologicalSort.fold(
  failure => ???,
  order   => ???
)

The result is of type TopologicalSort being a type alias for Either[TopologicalSortFailure, TopologicalOrder[NodeT]]. On failure, using the content of Left you have specific support to get a causing cycle. On success, Right contains the calculated TopologicalOrder represented by layers. When called at graph level, this will include all nodes irrespective of whether they are connected or they live in different components.

Combine your sort with fluent properties

To combine topologicalSort with any of the familiar fluent properties, call componentTraverser first like

graph.componentTraverser().withSubgraph(nodes = myNodeFilter).topologicalSort

Sort on node level

Whenever starting at a concrete inner node, topologicalSort() will only include nodes within the comopnent spanned by that node. In reverse, if you know your graph is connected you need not call TopologicalOrder at node level. It suffices to call it at graph level.

Note that node-level topologicalSort() also has a boolean argument allowing you to exclude predecessors from the result. Therefore, you always need to provide the paranthesis:

root.topologicalSort()

Sort on component level

Further, if you are interested in the topological order of the components of your graph, simply call

graph.componentTraverser().topologicalSortByComponent

that yields a Traversable[TopologicalSort], one for each component.

Exploit `TopologicalOrder`

TopologicalOrder is more than just a list of nodes. Most interestingly, you can call toLayered to lift this result type into a layered representation of the topological order:

graph.topologicalSort.fold(
  failure => yourFailureHandler,
  _.toLayered foreach println // prints topological order layer by layer
)

The layers of a topological sort can roughly be defined as follows:

layer 0 contains all nodes having no predecessors
layer n contains those nodes that have only predecessors in ancestor layers with at least one of them contained in layer n - 1.

Among others, layers are usefull to

compute several valid topological orders by altering the order of nodes within layers or
to maintain a stable ordering over JVM instances.

Cancel your traversal

To cancel a traversal

prefer calling one of scala.collection.Traversable's methods that stop the traversal as soon as the specified condition holds true such as exists or collectFirst
you may want to refer to the exception-based break() as provided by scala.util.control.Breaks
finally, return is also an option assumed you are familiar with its downside.

Build walks and paths

WalkBuilder and PathBuilder allow you to build a Walk respectively Path in terms of the underlying graph. This comes in handy whenever you have some results computed outside the library and would like to represent them by Graph for Scala path-dependent types. Since WalkBuilder and PathBuilder enforce proper walk/path semantics they are also well suited for checking user-supplied paths.

Here is how you can create a path in the sample graph above step by step by means of a PathBuilder:

val builder = g.newPathBuilder(n(1))
builder += n(3) += n(4)
builder.result().toOuterElems.toList // List[Outer](1, 1 ~> 3 % 5, 3, 3 ~ 4 % 1, 4)
   
builder.clear
builder += n(4) += n(3)
builder.result().toOuterElems.toList // List[Outer](1, 1 ~> 3 % 5, 3)
    
builder.clear()
builder add n(4)                    // false

As to

Instantiates a PathBuilder with the start node 1.
Adds the nodes 3 and 4 consecutively.
Tries to add the nodes 4 and 3 consecutively...
...but adding 4 gets refused since it is not a direct successor of 1.
You may want to check whether an addition was accepted by calling add instead of calling +=.

Note that it is also possible to create walks and paths by adding edges and, for multi-graphs, to define an edge selector.

Core User Guide: Traverse Your Graph

Traverse for a specific node, a path or a cycle

Refine traversers by properties

Ordering

Traverse for elements

Visit elements down and up

Extend visitors

Combine queries with visitors

Find components

Find weakly connected components

Find strongly connected components

To the type Component

Sort topologically

Sort on graph level

Combine your sort with fluent properties

Sort on node level

Sort on component level

Exploit TopologicalOrder

Cancel your traversal

Build walks and paths

To the type `Component`

Exploit `TopologicalOrder`