Core User Guide: Plan Your Graph

Nodes and edges

Presumably, you go for graphs because you have things that are connected, and you want to easily navigate along those connections. So the things become the nodes and their connections the edges. For instance, think of a graph describing relationships between persons. Persons become the nodes and their relations become the edges:

case class Person(name: String)

val g: Graph[Person, UnDiEdge[Person]] = ...

The node type.
A graph with node type Person and undirected edge type UnDiEdge. The predefined UnDiEdge suffices as long as you need a single type of relation between persons.

Simple enough, why should we waste time worrying about nodes and edges that are self-evident? Well, because real life often leaves you with different options.

Let's consider some options for modelling a database schema including

tables with their columns
indexes per table with a list of columns.

Intuitively, Tables and columns become nodes, edges represent which columns a table has. Next, what about indexes? Indexes could be modelled as another node type since they are kind of things, not just connections:

sealed trait SchemaObject
case class Table(name: String)  extends SchemaObject
case class Column(name: String) extends SchemaObject
case class Index(name: String)  extends SchemaObject

val g: Graph[SchemaObject, DiEdge[SchemaObject]] = ...

The node ADT.
The predefined directed edge class DiEdge may point
- from a table to the contained column or
- from an index to the contained column.

The above attempt has some deficiencies, though. First of all, there is no guarantee that nodes will be connected as expected. For instance, it is possible to add a directed edge from a column to an index. Such an arrow would result in a wrong set of adjacent nodes which should always be tables. Here is what we should prefer as a first improvement:

// ... (node ADT unchanged)

sealed trait Relation
case class TableColumn(table: Table, column: Column)
    extends AbstractDiEdge(from = table, to = column)
    with Relation
case class IndexColumn(index: Index, column: Column)
    extends AbstractDiEdge(from = index, to = column)
    with Relation

val g: Graph[SchemaObject, Relation] = ...

The ADT of edges.
These edge types are now typed with respect to the source and target nodes.
Note that, unlike DiEdge, Relation has no type parameter. Hence, we call such a graph typed graph.

Another drawback of the above design is that we missed relating indexes with tables. To overcome this issue in a property graph, you would use an edge labelled like IndexTable to be able to distinguish between arrows pointing to columns and arrows pointing to the table. Alternatively you could check that target node for its type. Keeping this in mind, let's move to the next drawback because once we get that resolved we also get rid of this IndexTable issue.

You have probably noticed, that an index is existentially bound to a table what is proven by the fact that if you drop a table, the index needs be dropped as well. In terms of a graph it feels a little strange if a node needs be dropped on dropping another node. Would it be more viable to model an index as an edge?

In fact, you can model indexes as hyperedges. In the database schema demo we play around with this approach, including Subset, but to start with take a look at the following simplified version:

sealed trait SchemaObject
case class Table(name: String)  extends SchemaObject
case class Column(name: String) extends SchemaObject

sealed trait Relation
case class TableColumn(table: Table, column: Column)
    extends AbstractDiEdge(from = table, to = column)
    with Relation
case class Index(table: Table, columns: OneOrMore[Column])
    extends AbstractDiHyperEdge(one(table), columns)
    with Relation

val g: Graph[SchemaObject, Relation] = ...

The ADT of nodes does not contain Index any more.
The edge type Index relates a table with a non-empty list of columns. OneOrMore is a data type supplied with Graph for Scala. It represents a list of at least one while Several represents a list of at leas two elements. OneOrMore and Several facilitate type-safe hyperedges because a directed hyperedge has one or more sources and also one or more targets while a hyperedge has at least two ends.

With this approach we have won the following:

Representing an index by a single directed hyperedge we got rid of unrelated directed edges per column that are much harder to maintain in a consistent way.
It suffices to inspect this single directed hyperedge to get all information about a specific index. In comparison, with directed edges per column you need to programmatically collect related nodes first to get the same information.
Once you remove a table from the graph, it's indexes will now be removed automatically.

With hyperedges at your fingertips, don't hesitate to take advantage of them whenever they improve your design.

Directed versus undirected

If the relation you plan to represent is symmetrical go for undirected edges or undirected hyperedges. To test for symmetry, just read the relation from both sides: If you end up with the same phrase from both sides your relation is symmetrical. For instance, in a road net locations are symmetrical tested by "I can drive from location A to location B and, likewise, I can drive from location B to location A." Let`s deal with one-way roads below.

As an example for asymmetrical relations, think of a person net that includes family as well as social relations. Then, parenthood is asymmetrical proven by "A is a parent of B and B is not a parent of A". B is rather a child of A. Also, assume you want to represent both parenthood and children in some way.

For asymmetrical relations, different options are viable. Concerning our example you may

use a directed edge for parenthood with the parent as the target. So you get the meaning depending on the direction you navigate. This assumes you can navigate into the opposite direction to get children what is supported by Graph for Scala, of course.
```
case class Person(name: String)

sealed trait Relation
case class Parent(child: Person, parent: Person)
    extends AbstractDiEdge(from = child, to = parent)
    with Relation
// ...more relations

val g: Graph[Person, Relation] = ...
        
```

use separate directed edges for parents and children. In this approach both directed edges need be present or absent with respect to two specific persons.

sealed trait Relation
case class Parent(child: Person, parent: Person)
    extends AbstractDiEdge(from = child, to = parent)
    with Relation
case class Child(parent: Person, child: Person)
    extends AbstractDiEdge(from = parent, to = child)
    with Relation
// ...more relations

irrespective of the asymmetric nature of the relation, use an undirected edge with the first end being the child and the second end being the parent. Here we assume that you can filter edges during traversals like "to get parents, navigate along with an edge only if its second end is different from the node to navigate from". However, since this solution seems rather tricky, we do not find it outstanding.
```
sealed trait Relation
case class Parent(child: Person, parent: Person)
    extends AbstractUnDiEdge(child, parent)
    with Relation
// ...more relations
        
```

use directed hyperedges for parents and children alike. Thus, both getting parents and getting children are pretty straightforward compared with gathering relevant non-hyper edges.

sealed trait Relation
case class Parents(child: Person, mather: Person, father: Person)
    extends AbstractDiHyperedge(sources = one(child), targets = OneOrMore(mather, father))
    with Relation
case class Children(parent: Person, children: OneOrMore[Person])
    extends AbstractDiHyperedge(sources = one(parent), targets = children)
    with Relation
// ...more relations

Labelled edges

Most often you also need some edge label. Feel free to add any number of fields to your typed edge for this purpose. In terms of our above database schema example, we could add a "unique" property to the Index edge like:

case class Index(table: Table, columns: OneOrMore[Column], unique: Boolean)
    extends AbstractDiHyperEdge(one(table), columns)
    with Relation

As a second example, we could extend the above Parent edge like

case class Parent(child: Person, parent: Person, `type`: ParenthoodType)
    extends AbstractDiEdge(from = child, to = parent)
    with Relation

with ParenthoodType being an enumeration like {Biological, Adoptive, Surrogate...}.

In case you are still wondering, here is why we refrain from providing generic labelled edges:

Whenever you define a typed edge, what we recommend anyway, you may also add any number of labels in one go.
Adding yet another type parameter for the label would increase complexity.
With heterogeneous graphs in mind, typed edges are fully flexible with respect to different edge types. A type parameter for the label would only be a good pick for homogeneous graphs.
With typed edges you can use proper names for your label fields. You don't need any redirection by an artificial field called label.

Mixed graphs

You are free to mix any combination of directed, undirected and hyperedges in the same graph. Just look up the lowest common ancestor of your edge types in

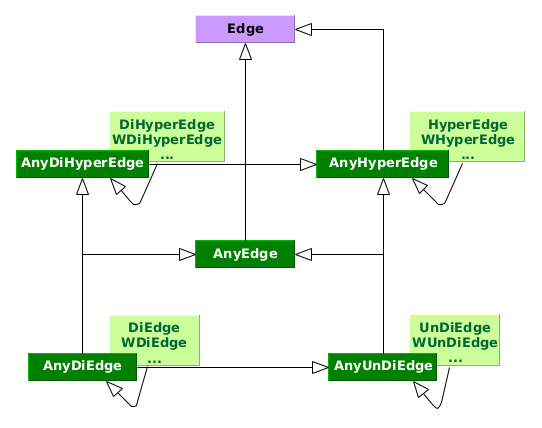
and use the corresponding abstraction with the prefix Any like

sealed trait Relation extends AnyEdge[Person]

case class Parent(child: Person, parent: Person)
    extends AbstractDiEdge(from = child, to = parent)
    with Relation
case class Friends(one: Person, another: Person)
    extends AbstractUnDiEdge(one, another)
    with Relation

val g: Graph[Person, Relation] = ...

AnyEdge is the lowest common ancestor of DiEdge and UnDiEdge.

Mixed graphs work for generic and typed edges alike.

Multigraphs

The previous example graph supporting edges of the type Parent or Friends works fine. You can connect two given Persons with a single edge or both Parent and Friends while you cannot connect them by more than one edge of the same type like Friends. This is the case because AbstractDiEdge and AbstractUnDiEdge apply a different built-in equality with respect to the same nodes. In specific,

directed and undirected edges connecting the very same nodes never equal
a directed edge with their nodes swapped is not equal to the original edge
an undirected edge with their nodes swapped is equal to the original edge
for hyperedges different strategies are supported.

But what happens if we add yet another edge type?

case class Siblings(one: Person, another: Person)
    extends AbstractUnDiEdge(one, another)
    with Relation

Now Friends and Siblings have the same equality, so you will not be able to connect the same nodes by both edge types. To resolve this conflict mix in MultiEdge which serves to extend equality:

case class Friends(one: Person, another: Person)
    extends AbstractUnDiEdge(one, another)
    with MultiEdge
    with Relation {
  def extendKeyBy = OneOrMore.one(Friends)
}
case class Siblings(one: Person, another: Person)
    extends AbstractUnDiEdge(one, another)
    with MultiEdge
    with Relation {
  def extendKeyBy = OneOrMore.one(Siblings)
}

The mix-in MultiEdge requires extendKeyBy to be implemented. Defining a single constant key suffices here.
Same as with Friends but we need a different constant. Using constants ensures that you cannot connect two given Persons by the same edge type more than once.

In contrast, whenever you need to allow for several edges of the same type between two given nodes you would implement extendKeyBy by referring to some discriminator value specific to edge instances. For instance, were you also keeping track of Meetings between Persons, you could go with something like

case class Meeting(a: Person, b: Person, time: Datetime)
    extends AbstractUnDiEdge(a, b)
    with MultiEdge
    with Relation {
  def extendKeyBy = one(time)
}